For the reciprocal squared function latexf\left(x\right)=\frac{1}{{x}^{2}}/latex, we cannot divide by latex0/latex, so we must exclude latex0/latex from the domain There is also no latexx/latex that can give an output of 0, so 0 is excluded from the range as well Note that the output of this function is always positive due to the square in the denominator, so the rangeFind the range and the domain write the range and domain using interval notation Precalculus The function f has a domain of 0,5and a range of 0,3 Start by sketching a potential graph of f Suppose the function k is defined as k(x)=f(x−3) Determine the domain and range of k Domain Range2107 · Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
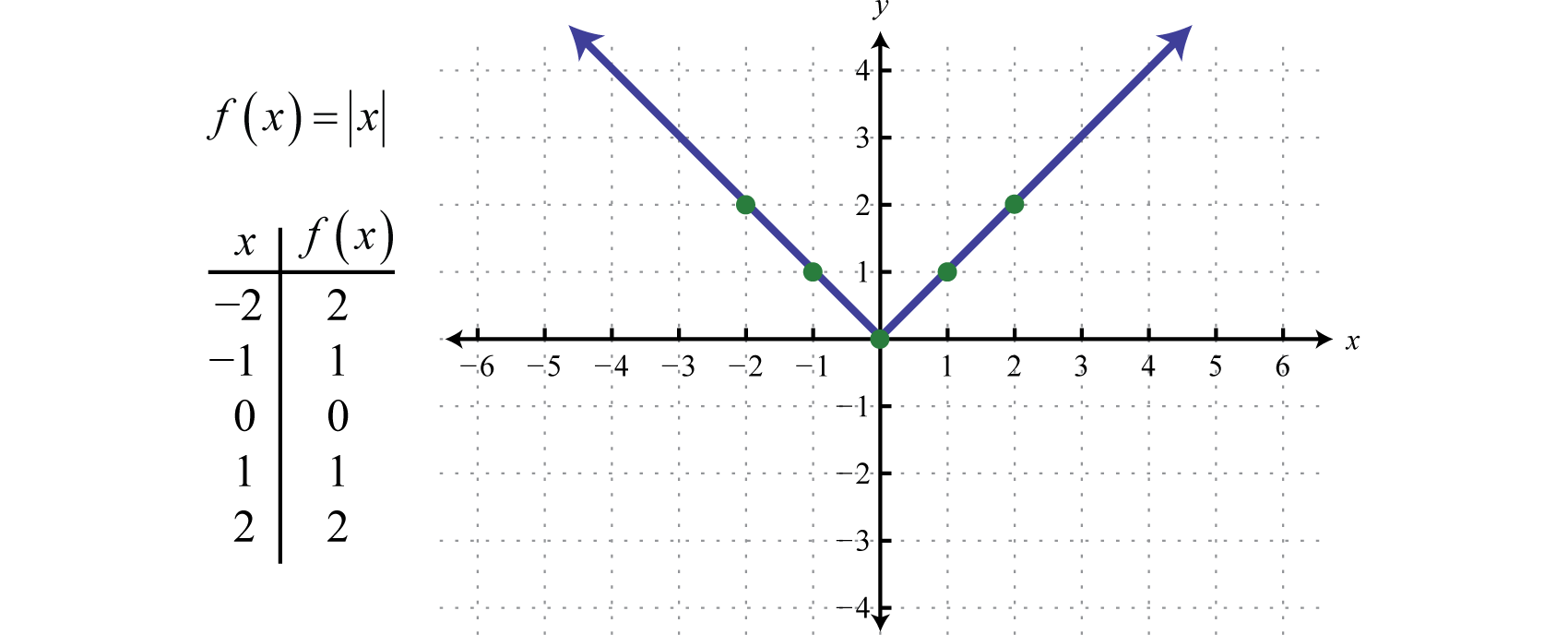
Graphing The Basic Functions
F(x)=x^2+1 domain and range
F(x)=x^2+1 domain and range-This is the Solution of Question From RD SHARMA book of CLASS 11 CHAPTER RELATIONS AND FUNCTIONS This Question is also available in R S AGGARWAL book of CLASFind Domain and Range of real functions (1) `f(x)=(x2)/(3x)` (2)`f(x)=1/sqrt(x5)` (3) `f(x)=x/(1x^2)`



Find The Domain And Range F X 2x 2 Displaystyle F Left X Right 2 X 2 Snapsolve
Some general tips Division by zero is not allowed) As an example, let's say you have the function f(x) = 1/(x 2 – 9) You can exclude any values of x (the domain) that make the denominator equal to zero0309 · A function is expressed as y=f(x), where x is the independent variable and y is the dependent variable First, we learn what is the Domain before learning How to Find the Domain of a Function Algebraically 👉 What is the Domain of a Function?Let f(x) be a realvalued function Then the domain of a function is the set of all possible values of x for which f(x) is defined
–1 x 2 4 y 021 Mathematics Learning Centre, University of Sydney 5 State its domain and range Solution The function is defined for all real xThe vertex of the function is at (1,1) and therfore the range of the function is all real y ≥ 1 12 Specifying or restricting the domain of a functionX = 2 The x intercepts is at the point (2 , 0) b The domain of f is the set of all real numbers Since x 2 is either positive or zero for x = 2;09 · Given f (x) = 1/√x−5 To find the domain and range of function Explanation So, the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f (x) = 1/√x−5 Now for real value of x5≠0 and x5>0 ⇒ x≠5 and x>5 Hence the domain of f = (5, ∞)
The domain is 0;1 as is the range (e) f(x) = x2 2x 3 The domain is R as f(x) is de ned for all values of x We now examine the range ie what values do we get from x22x3 as xvaries over all the domain ie over all values?Which is the level curve f(x;y) = 75 in the function's domain P Sam Johnson Domains and Ranges of Functions of Several Variables 23/78The domain and range of the function f= ((1/1x2)) x ∈ R, x ≠ ± 1 are respectively Q The domain and range of the function $f=\left\{\left(\frac{1}{1x^{2}}\right) x \in R, x
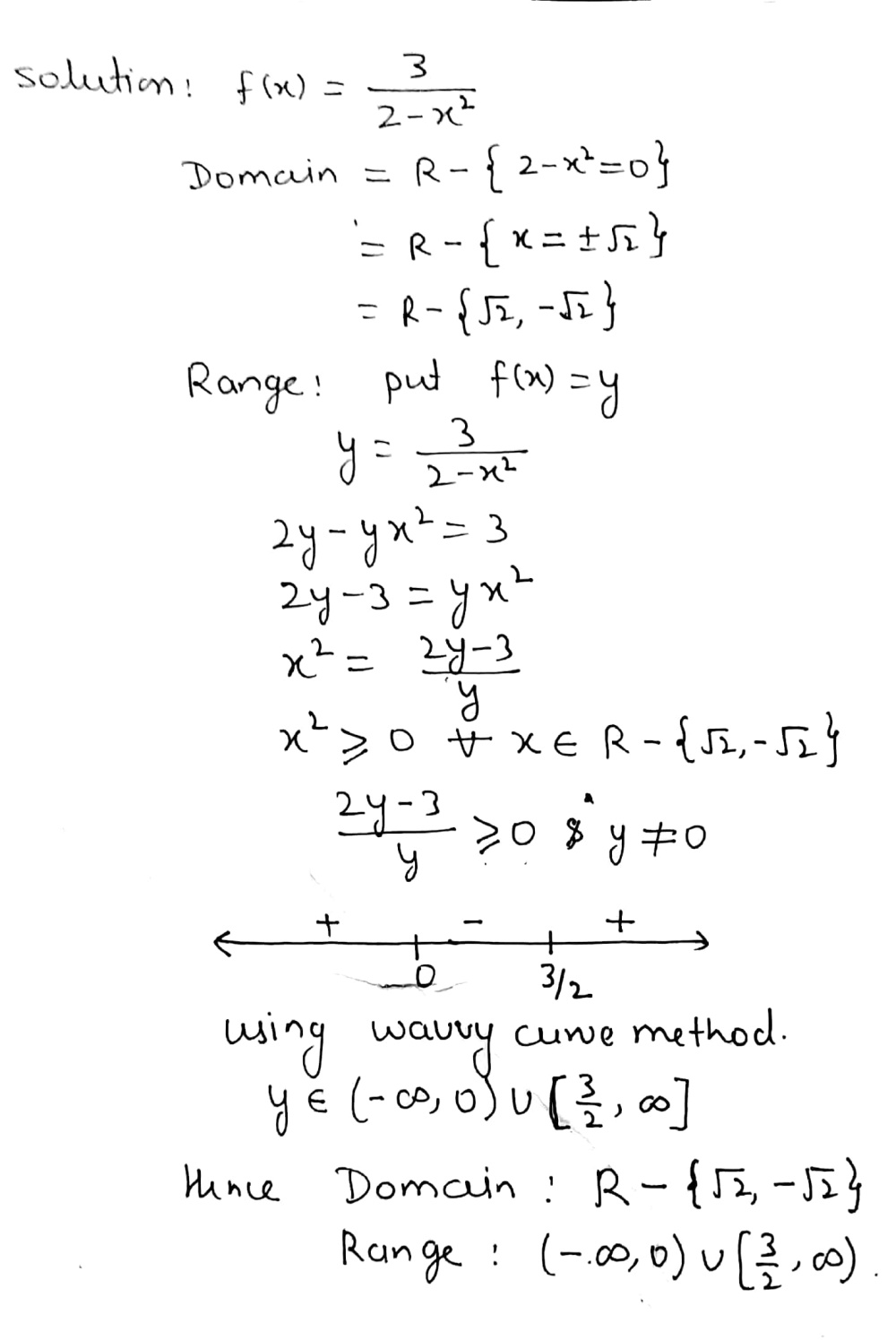



Find The Domain And The Range Of The Function F Left X Right Frac 3 2 X 2 Snapsolve




Let F X Y Z 1 X 2 Y 2 Z 2 Find The Domain Chegg Com
Answer The domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y valueArithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal domain\y=\frac{x}{x^26x8} domain\f(x)=\sqrt{x3} domain\f(x)=\cos(2x5) domain\f(x)=\sin(3x) functiondomainAnswer to Describe the domain and range of the function f(x, y) = x^2 y^2 By signing up, you'll get thousands of stepbystep solutions to your



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic




Find Domain And Range Of F X X 1 X 2
Answer to Let f(x) = square root{x^24}, g(x) = x^2/x^21, find (f/g) (x) and state the domain By signing up, you'll get thousands of · The given function is f (x) = 2x 4 we have to find the domain and range of the function Domain of the function will be ∞ ≤ x ≤ ∞ or (∞, ∞) {x x ∈ R} Range of the function is represented on y axis that will be 0, ∞) {y y ≥ 0} searchInformally, if a function is defined on some set, then we call that set the domain The values taken by the function are collectively referred to as the range For example, the function x2 x 2 takes the reals (domain) to the nonnegative reals (range)




Find The Domain And Range Of The Real Function F X Sqrt 9 X 2 Youtube




How To Find The Domain And Range Of A Function 14 Steps
· Find the domain and range of f (x)=x2/1x2 Domain of the function is where the function is defined The given function X R Let fx y y x1x2 x y1 x2 yx2 x y 0 This is quadratic equation with real roots Find the domain and range ƒx 1 x2 Maintain the following steps 1 QUESTION 2 Find the domain of the function fxy1500 · ️Given real function is f(x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R ️Let f(x) = y ️y = x/1x^2 ️⇒ x = y(1 x^2) ️⇒ yx^2 – x y = 0 ️This is quadratic equation with real roots ️(1)^2 – 4(y)(y) ≥ 0 ️1 – 4y^2 ≥ 0 ️⇒ 4y^2 ≤ 1 ️⇒ y^2 ≤1/4F(x) = `sqrt(16 x^2)` For f to be defined, 16 – x 2 ≥ 0 ∴ x 2 ≤ 16 ∴ – 4 ≤ x < 4 ∴ Domain of f = – 4, 4 Clearly, f(x) ≥ 0 and the value of f(x) would be maximum when the quantity subtracted from 16 is minimum ie x = 0




Find The Domain And Range Of The Function Defined By F X 1 9 X Please Help Me Brainly In
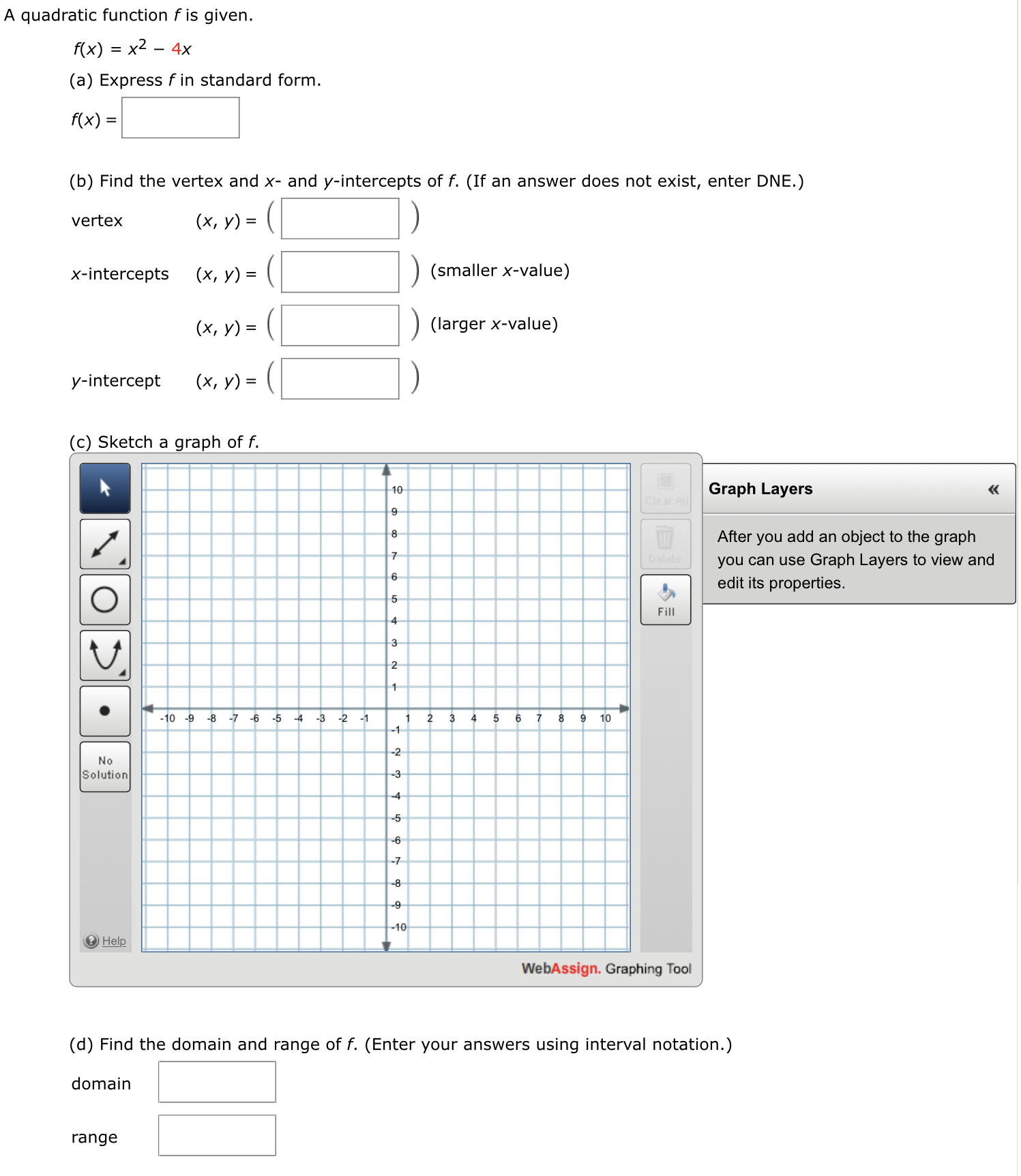



Answered A Quadratic Function F Is Given F X Bartleby
2801 · Ex 23, 2 Find the domain and range of the following real function f (x) = –x Here we are given a real function Hence, both domain and range should be real numbers Here, x can be any real number Here, f (x) will always be negative or zero All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All realDomain and range of z = x^2 y^2 Extended Keyboard; · f (x)= x^2 5 The domain are all x values that has images As you see, we do not have any restrictions on the values of x ==> Therefore, the domain is all real numbers As for the range




Find Domain And Range Of Function Let A 2 1 0 1 2 And F A Gtz Be Given By F X X 2 2x Youtube




If F X X 2 X X 2 2x Then Find The Domain And Range Of F Show That F Is One One Youtube
Find the Domain and Range f (x)=x^21 f (x) = x2 1 f ( x) = x 2 1 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval NotationThe range of f is given by the interval 0 , infinity) c To sketch the graph of f (x) = x 2, we first sketch the graph of y = x · Determine the domain and range of the function f (x) = 2 RootIndex 3 StartRoot 108 EndRoot Superscript 2 x




Find The Domain And Range F X 2x 2 Displaystyle F Left X Right 2 X 2 Snapsolve




Find The Domain And The Range Of The Function F X X 2 25 X
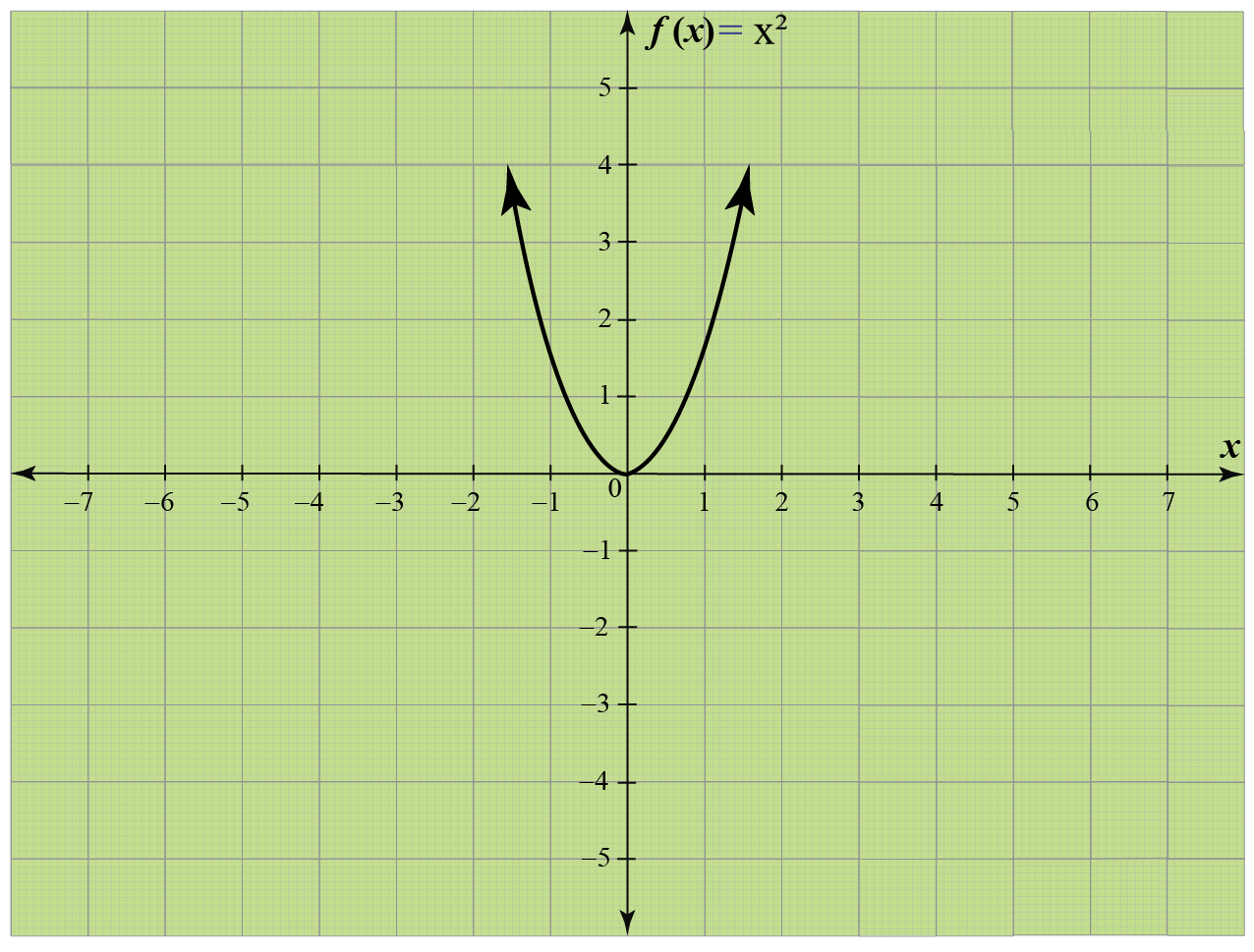
Find the Domain and Range f (x)=x^2 f (x) = x2 f ( x) = x 2 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x xThe gure shows the contour curve f(x;y) = 75 on the surface z = 100 x2 y2 de ned by the function f(x;y) = 100 x2 y2 The contour curve lies directly above the circle x2 y2 = 25;F (x) = x 2 The function f (x) = x2 has a domain of all real numbers ( x can be anything) and a range that is greater than or equal to zero Two ways in which the domain and range of a function can be written are interval notation and set notation




Find The Domain And Range Of F X 2 5x 3x 4
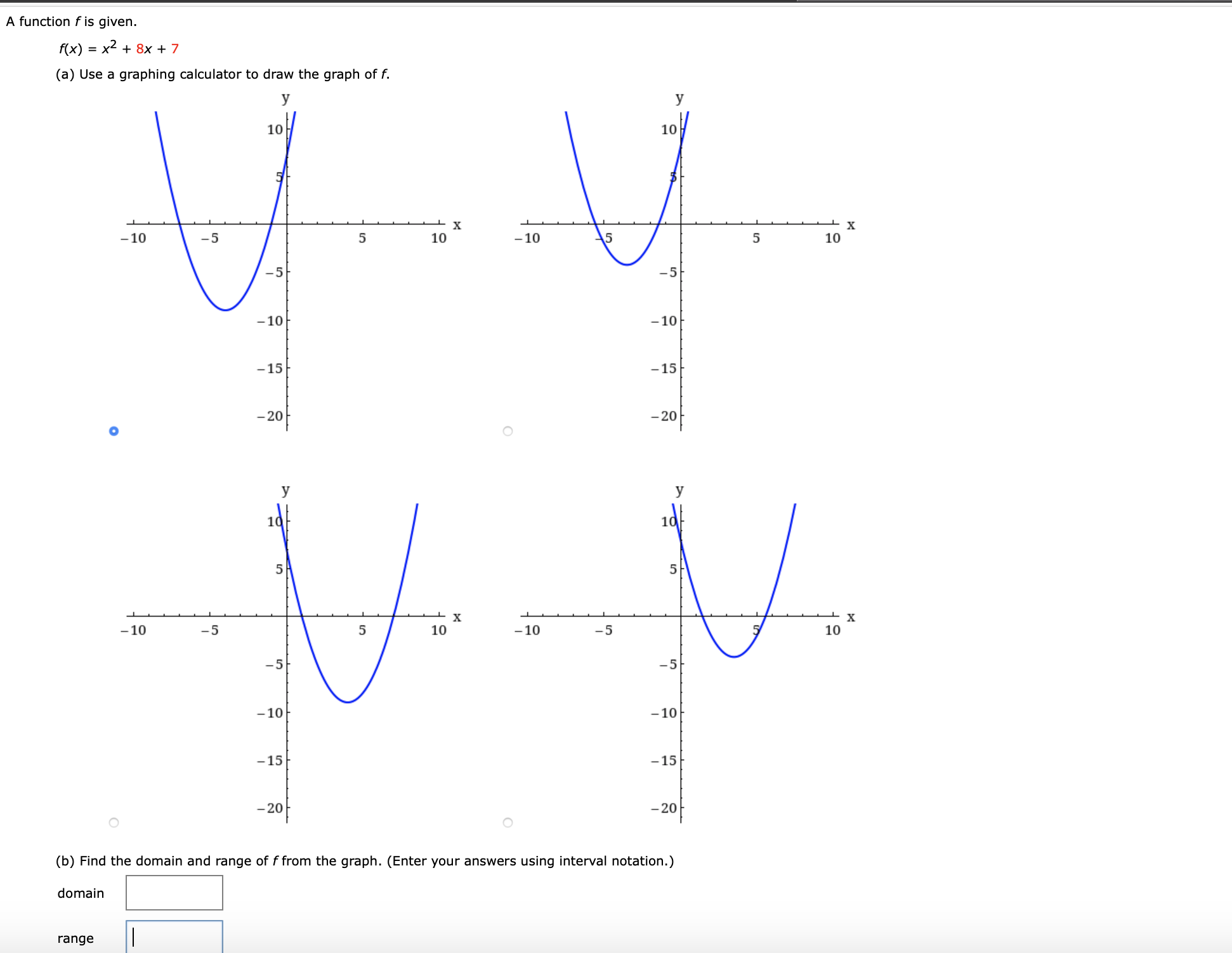



Answered A Function F Is Given F X X2 8x Bartleby
1113 · domain/range of the inverse of the given function f(x)=7x^2 ;Here is what I didThe domain of f (x)=2^x would be the x values This would include all values that you can input as x in order to make this problem work The domain of a function is usually all real numbers The range of f (x)=2^x would be the y valuesDoman= R,Range= (−∞,2 Given f (x)= 2−∣x−5∣ Domain of f (x) is defined for all real values of x Since, ∣x−5∣ ≥0 −∣x−5∣ ≤0 2−∣x−5∣ ≤2 f (x) ≤2 Hence, range of f (x) is (−∞,2




Find The Domain And Range Function F X X 2 3x 2 X 2 4x



Domain And Range Ppt Download
Clearly the given function f (x) = 2 x 4 is defined for all real numbers and always >/= 0 Therefore its domain is the complete set of real numbers ie R Since the function is always >/=0 therefore its range is 0, infinity) that is set of non negative real numbersCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyFirst we should define the function in interval Since there is square root, math9x^2 >=0/math math(3x)(3x)>=0/math math(3x)(x3)




Find The Domain And Range Of The Function F X Root 4 X 2 And X Belongs To R Maths Relations And Functions Meritnation Com




Solved Find The Domain And Range If F X 2x 3 2x 2 An Chegg Com
· The domain and range of the function f(x) = x 2 has to be determined The domain of a function is all values of x for which the value of f(x) is definedFor quadratics like this it is a good idea to complete the squareThe same applies to the vertical extent of the graph, so the domain and range include all real numbers Figure 18 For the reciprocal function f ( x) = 1 x , f ( x) = 1 x , we cannot divide by 0, so we must exclude 0 from the domain Further, 1 divided by any value can never be 0, so the range also will not include 0




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2




What Is The Domain Of The Function F X 1 X X
Domain and range graph The graph of f(x)=x2 f ( x) = x 2 (red) has the same domain (input values) as the graph of f(x)=− 1 12x3 f ( x) = − 1 12 x 3 (blue) since all real numbers can be input values However, the range of the red graph is restricted to only f(x)≥0 f ( x) ≥ 0, or y y values above or equal to 0 0Basically, use your algebra skills to find the domain and range for a function by guessing and checking!1009 · We have f(x) = (x 2 9)/(x 3) Domain off Clearly f(x) is not defined for x – 3 = 0 ie x = 3 Therefore, Domain (f) = R – {3} Range off Let f(x) = y Then, f(x) = y (x 2 9)/(x 3) = y x 3 = y It follows from the above relation that y takes all real values except 6 when x takes values in the set R – {3} Therefore, Range (f



11th Domain And Range Of Squre Root Of 9 X2 Youtube



Domain Range A Function
Solution For Find the domain and range of f(x) = 1x 2 So, Range will be all the values less than or equal to zeroF (x)=sqrt (x2) Answer by edjones (8007) ( Show Source ) You can put this solution on YOUR website!Find the domain and range of the function $$f(x) = \sqrt{x^2 25} $$ and $$ f(x) = \sqrt{25 x^2}$$



Domain Range A Function




Misc 5 Find Domain And Range Of F X X 1 Class 11
· Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe domain is x 2, infinity) square root of a negative number is not allowed The range is y 0, infinity) EdAnswer (a) For any real values of x the function will not be undefined So, the domain is a set of all real numbers (b) Range of f (x) is also a set of all real numbers (c) In order to find the inverse function, first we have to prove the given function is one to one Every different values of x is associated with unique values of f (x)




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In
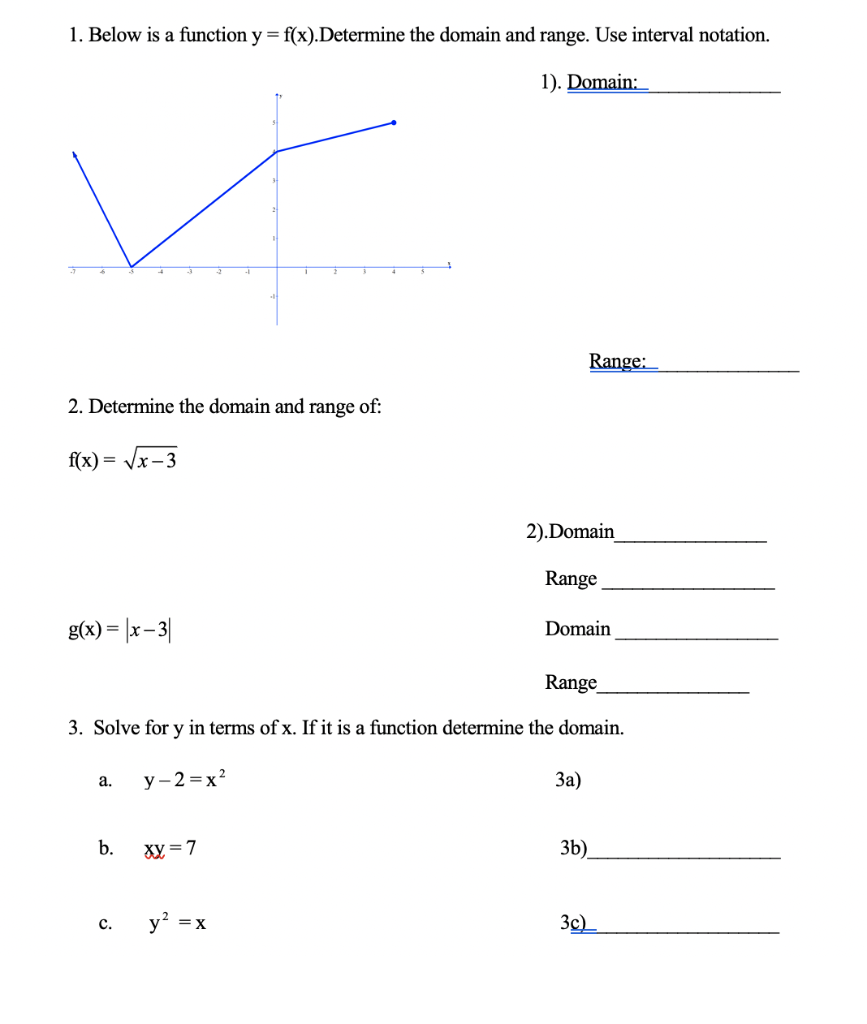



Solved 1 Below Is A Function Y F X Determine The Doma Chegg Com
X greater than or equal to 0 asked Nov , 13 in ALGEBRA 1 by angel12 Scholar domainofafunction




Find The Domain And Range Of The Real Function Defined By F




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube




Find Domain Sq Rt 2x 1 3and Range Of Square Root Function And Its Inverse Youtube
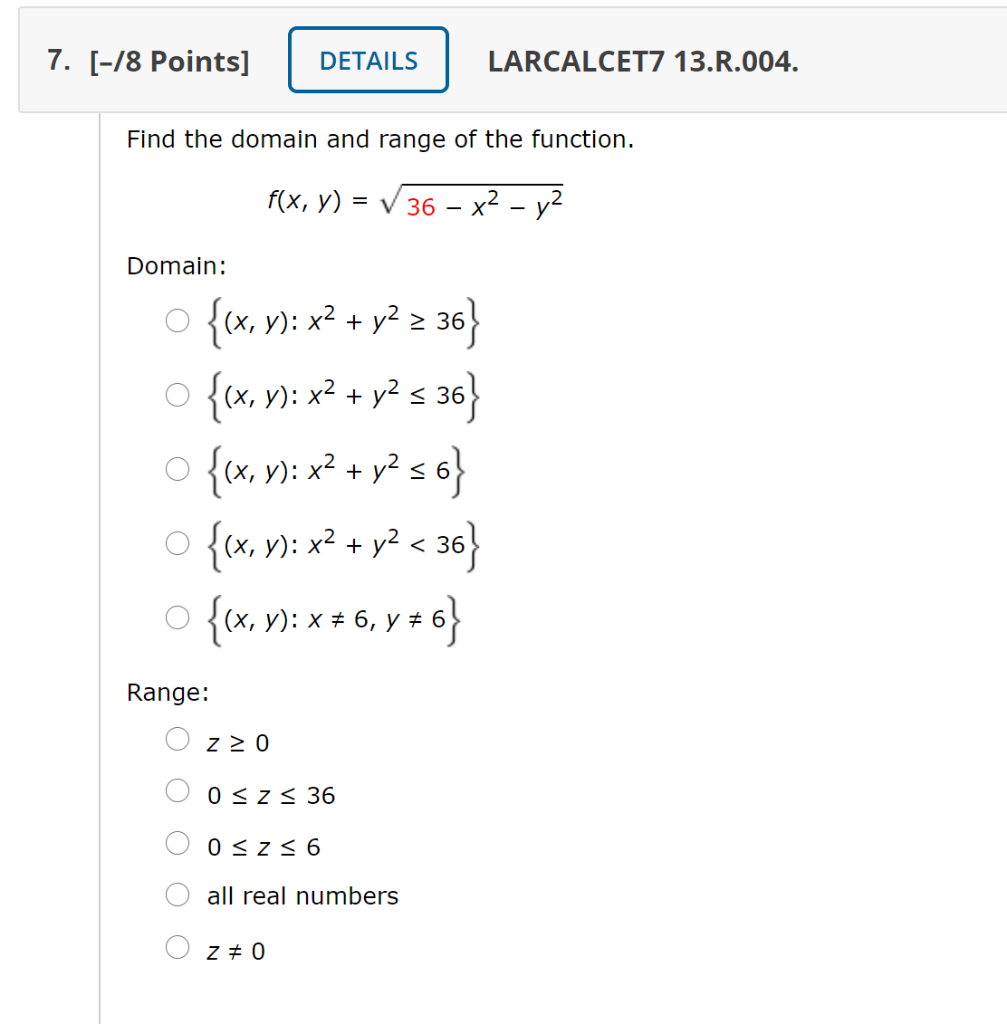



Solved 7 8 Points Details Larcalcet7 13 R 004 Find Chegg Com
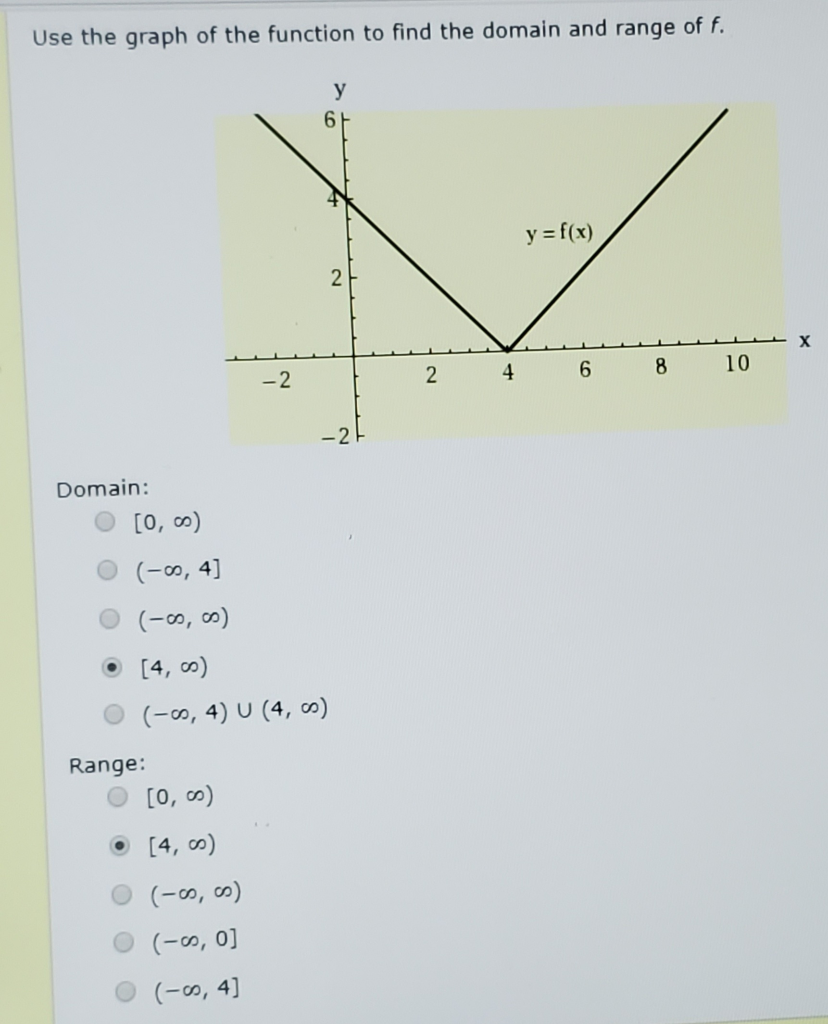



Use The Graph Of The Function To Find The Domain And Chegg Com
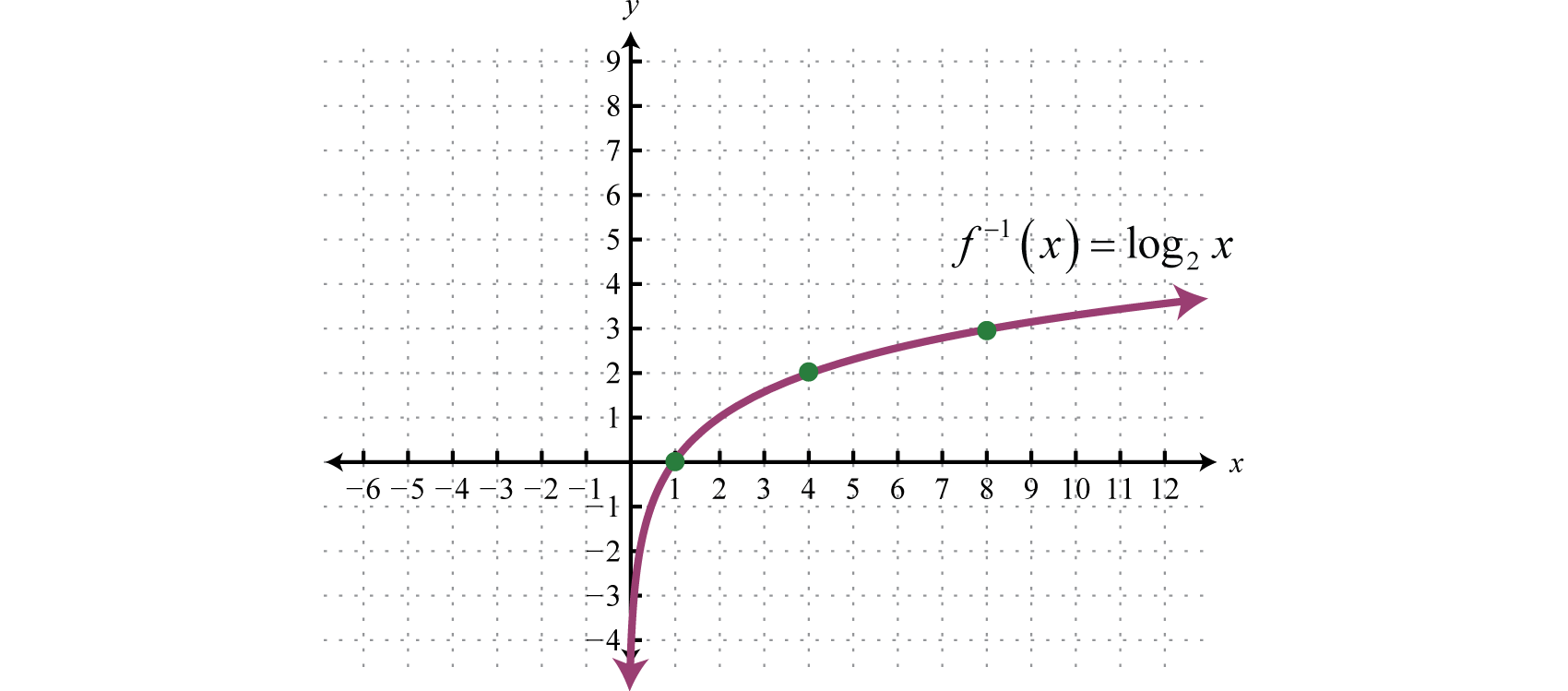



Logarithmic Functions And Their Graphs




6 Ways To Find The Domain Of A Function Wikihow




The Range Of The Function F X Sqrt 5 X 2 6 Is 3 2 Uu 2




F X X 2 16 X 4find The Domain And Range




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X



Domain Definition Examples Cuemath




Find The Domain And Range Of F X 1 Sqrt X 2




Find The Domain Amp Range Of F X 2 3x 2 Also Find F 2 Brainly In




Section 7 2b Domain And Range Ppt Download




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2




Find The Domain And Range Of The Function F X X 1 X 2 Brainly In




Domain And Range Of 1 X 2 2x 8 Youtube




Graphing The Basic Functions




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




Find The Domain And Range Of F X 9 X 2 Brainly In




Find The Domain And Range Of F X 3 2 X 2 Brainly In




Find The Domain And Range Of Each Of The Following Real Value Functions F X X 22 X




Find The Domain And The Range Of The Function F X X 2 25 X 5 Youtube




Find The Domain And Range Of The Function F X Sin 1 X 2




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube
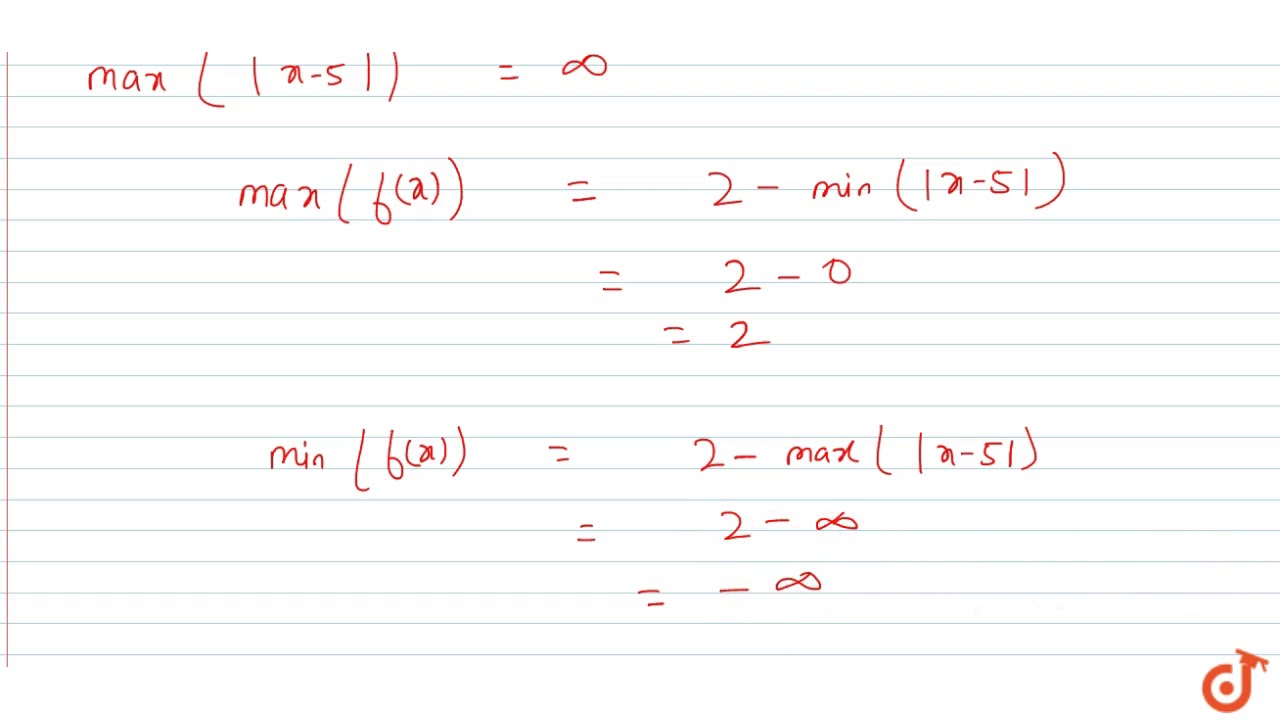



The Domain And Range Of The Function F Given By F X 2 X 5 Is Youtube




Find The Domain And Range Of F X 2x Cos X
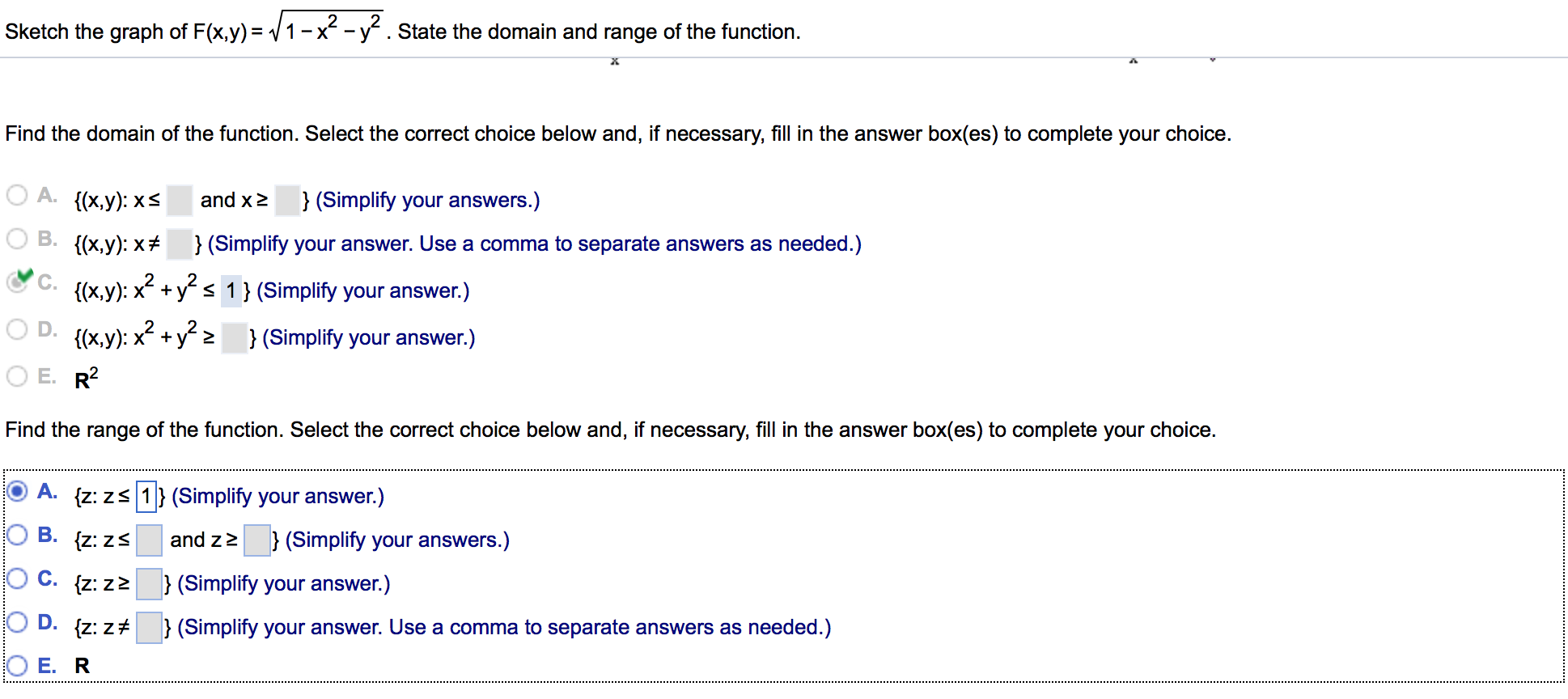



Solved Sketch The Graph Of F X Y Squareroot 1 X 2 Chegg Com




Draw The Graph Of F X X 2 And Write Its Domain And Range Maths Relations And Functions Meritnation Com
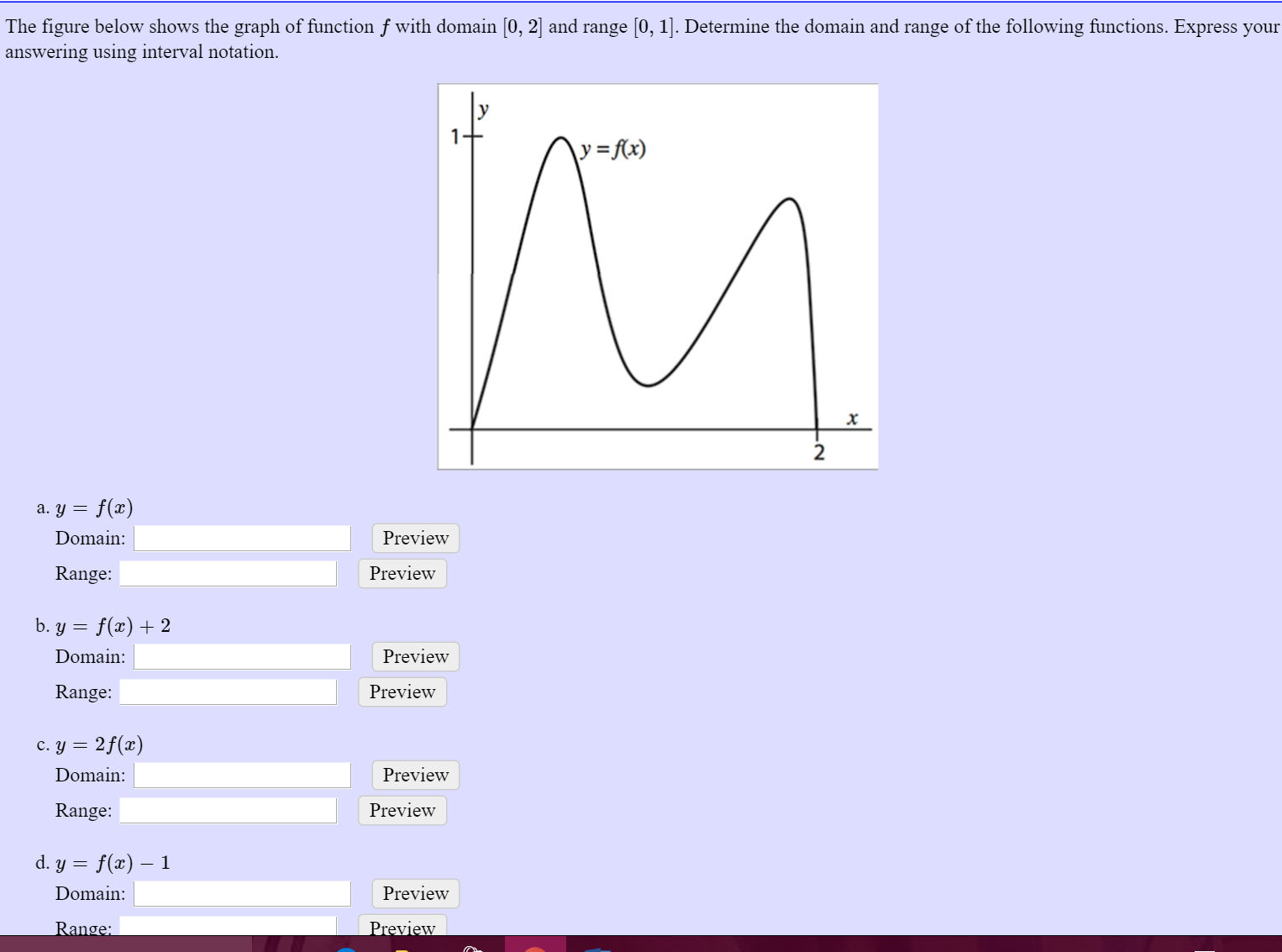



Solved The Figure Below Shows The Graph Of Function F Wit Chegg Com
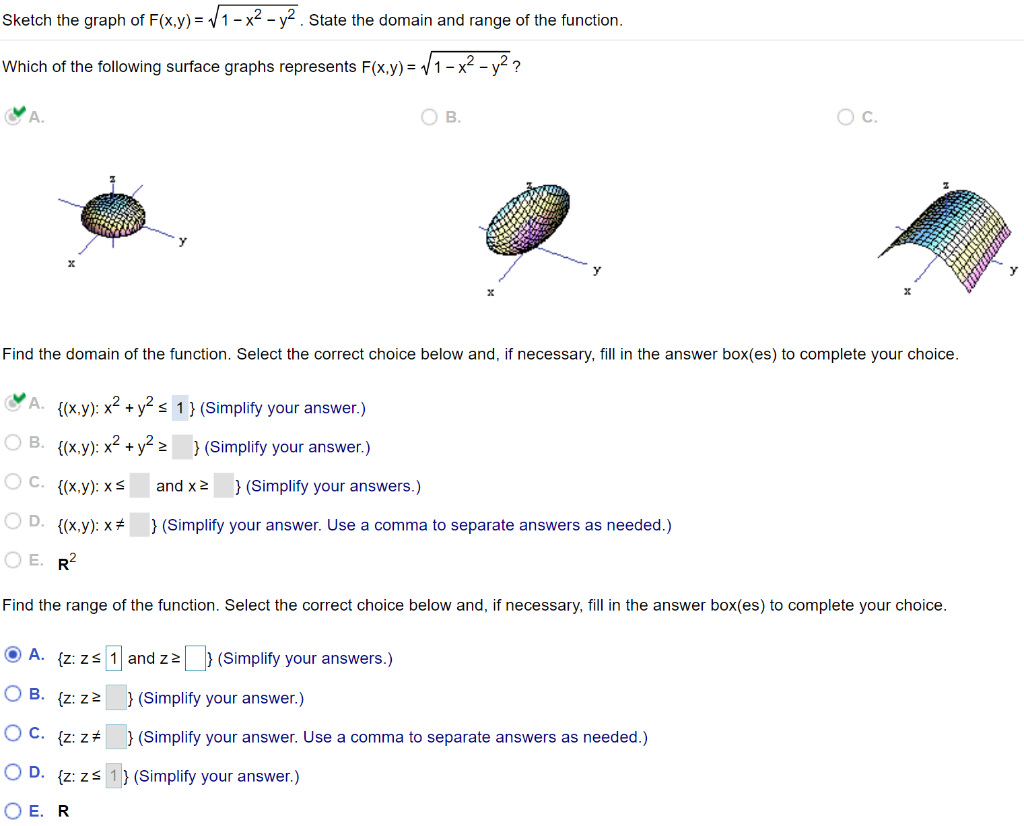



Solved Sketch The Graph Of F X Y Sqrt 1 X 2 Y 2 State Chegg Com




Answered 5 The Function F X 2 75x2 Models Bartleby




Determine The Domain And Range Of The Following Function Record Your Answers In Set Notation The Brainly Com
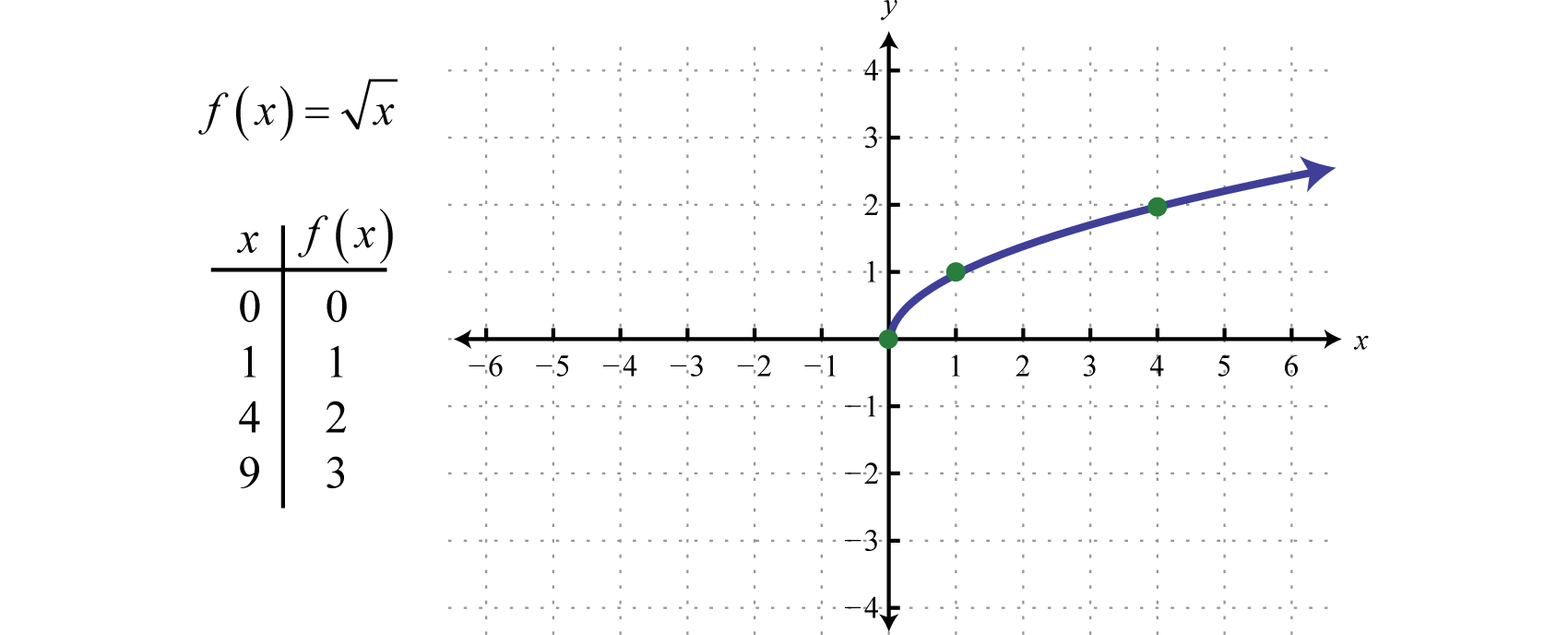



Graphing The Basic Functions




Domain And Range Of Quadratic Functions Video Khan Academy




4 Ways To Find The Range Of A Function Wikihow




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange




Find The Domain And Range Of Each Of The Following Real Value Functions F X X 2 16
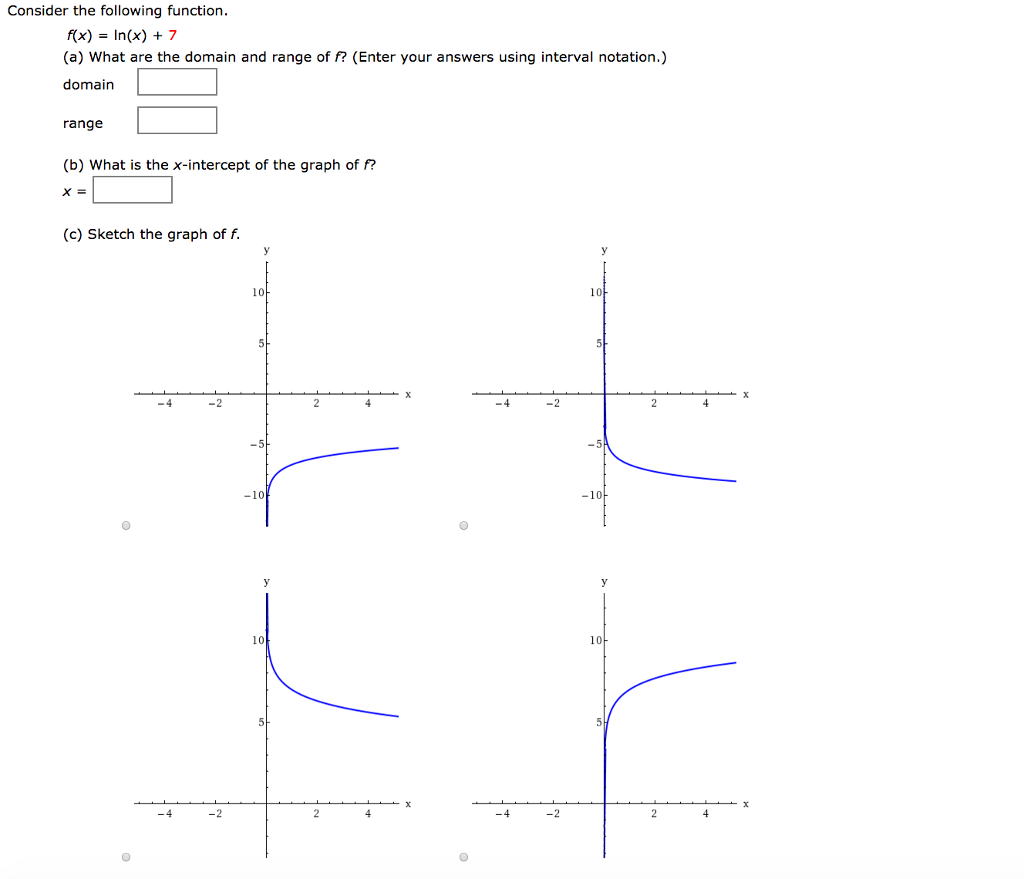



Consider The Following Function F X Ln X 7 Chegg Com
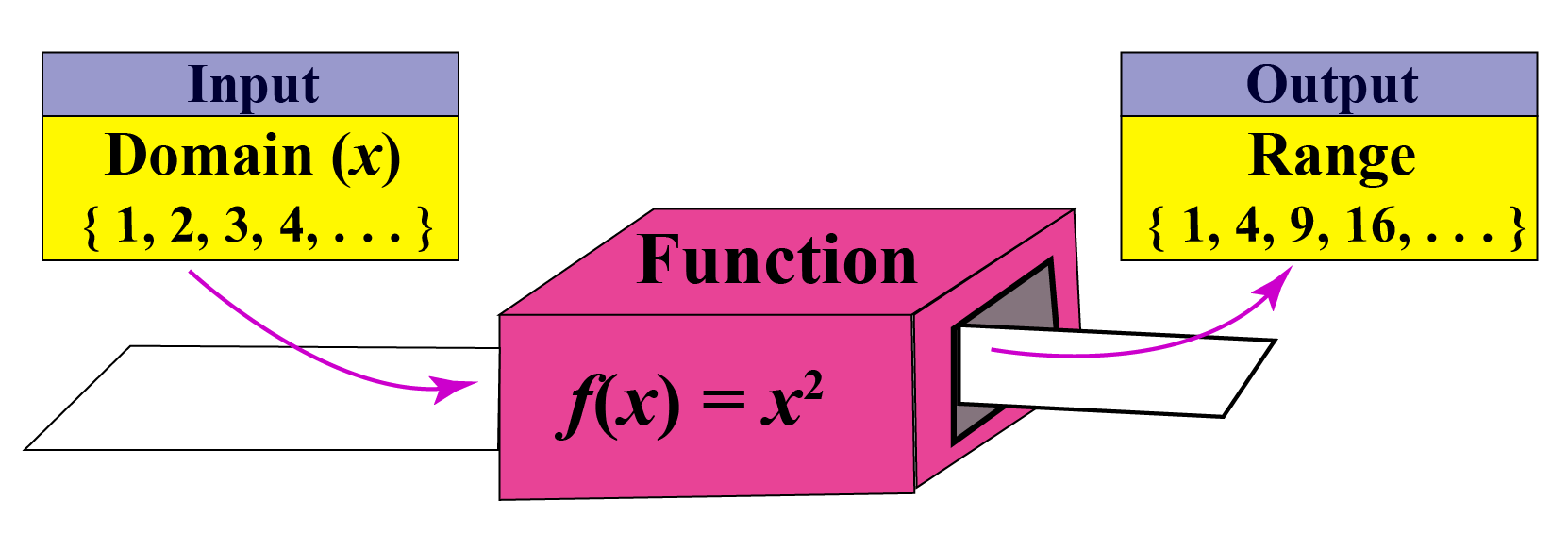



Domain Range Of Functions Graphs Calculator Examples Cuemath




Find The Domain And Range Of F X X Sgn X Youtube




Rd Sharma Solutions For Class 11 Chapter 3 Functions Download Free Pdf




Domain Range Of Functions Graphs Calculator Examples Cuemath




Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12




Find The Domain And Range Of F X Square Root Of X 2 3x 2 Maths Relations And Functions Meritnation Com



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora




Find The Domain Range Of F X 1 9 X 2 Brainly In




If The Domain Of The Function F X X 2 6x 7 Is Oo Oo Then The Range Of The Funct Youtube
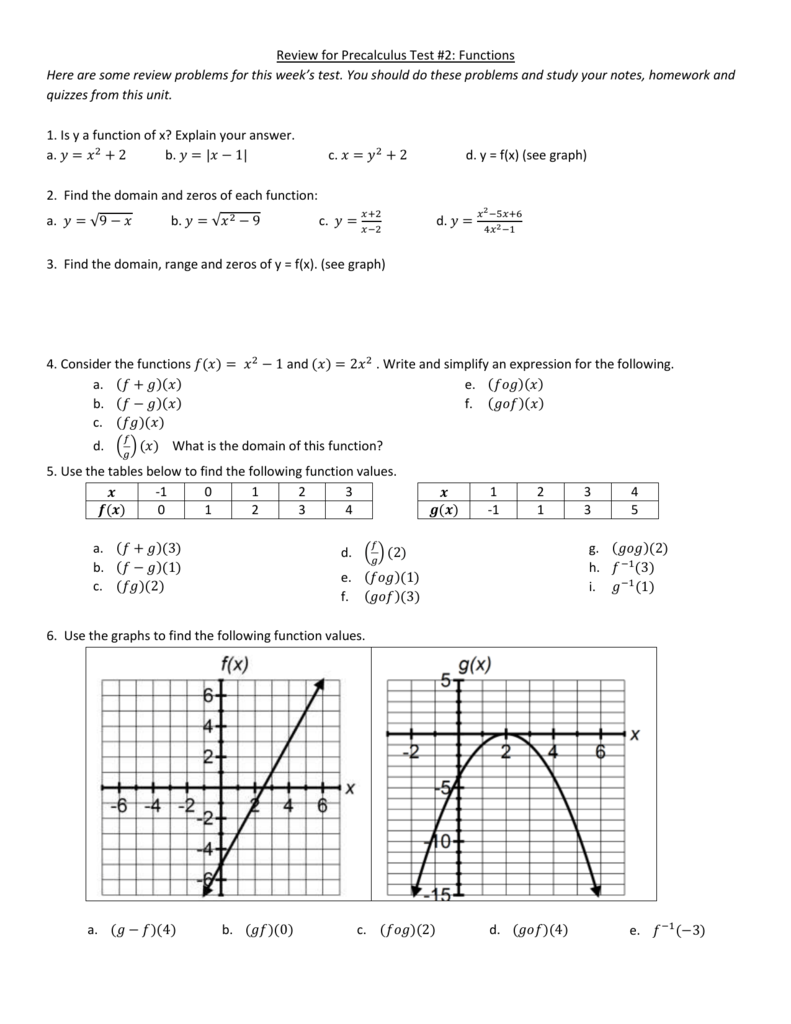



Review For Precalculus Test 2 Functions Here Are Some Review




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange



A1 Find And Graph The Inverse See How To Solve It At Qanda
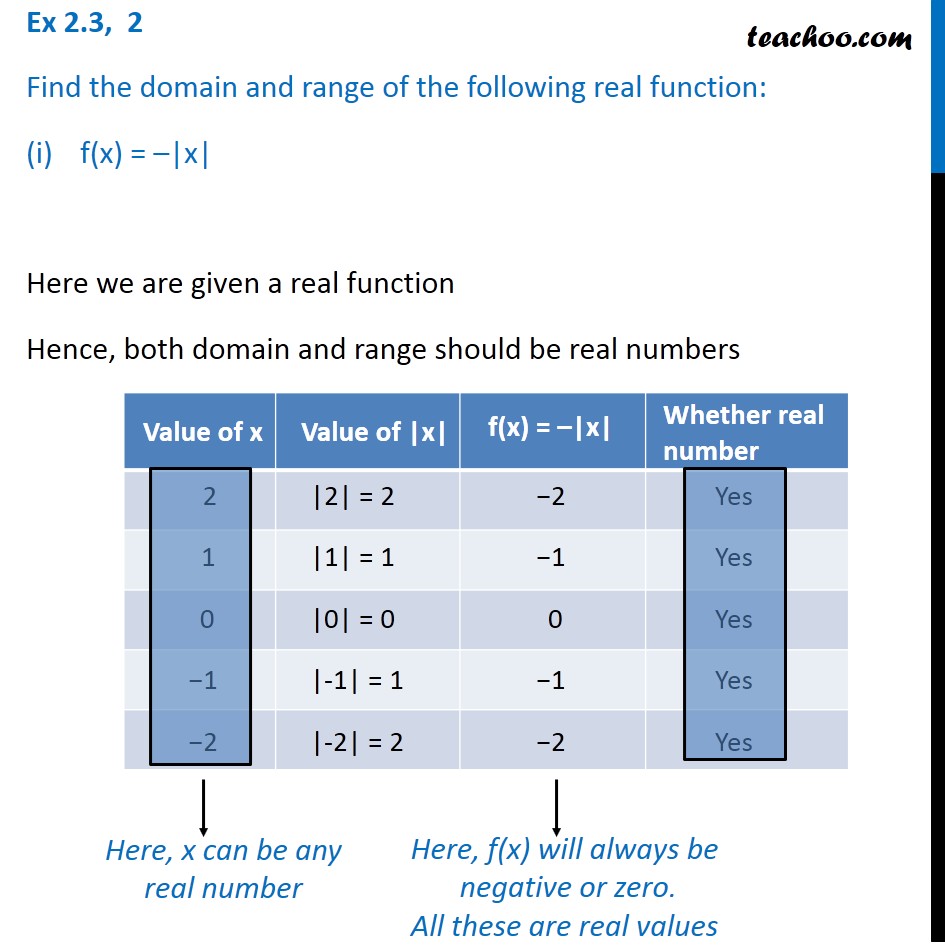



Ex 2 3 2 Find Domain And Range I F X X Chapter 2




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic




Igcsefm Domain Range Ppt Download




Consider The Function F X X 1 C 2x 8 2x 8 C X 1




Question Video Determining The Domain And Range Of A Quadratic Function Nagwa




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube



Relations Graphs And Functions



Warm Up Linear Equations Multiple Choice Learning Targets Ppt Video Online Download




Find The Domain And Range Of The Function F X 1 1 X 2 X I




F X Square Root Of X 2 16 Find Domain And Range Brainly In




Find The Domain And Range Of The Function F X 1 X 5 Donimain




Find The Domain And Range Of Real Function F X 4 X 2 Brainly In




Domain And Range Of Quadratic Functions Video Khan Academy




Find The Domain And Range Of The Function F X X 2 9 X 3



0 件のコメント:
コメントを投稿